Fractal dimension of natural objects from nano-to macro-scale: an intrinsic property of material
SummaryMany natural objects are innately composed of complex geometric figures, termed as fractals, and their mathematics are extremely complicated. The complexity and beauty found in these fractals has inspired several researchers to create them using mathematical formulations and computer aided graphics tools and software. These designs generated in various forms and psychedelic colours have become a digital art medium for design of wall papers, animation movies, fabric printing etc. However, there are simple experiments and simulations to comprehend it. Here, we demonstrate a simple experiment from the literature to estimate the fractal dimension of crumpled paper balls, and also discuss a method for aerosols.
Fractals - an intrinsic property of materialA fractal is an object or a mathematical entity exhibiting self-similarity across different scales, with a seemingly never-ending pattern. Examples of fractals from physical world around us are cauliflower (Fig.1), ferns, trees, rivers, coastlines, mountains, clouds, seashells, hurricanes, etc. The typical well-cited example to understand the concept of a fractal is that of the coastline. The length of the coastline is highly dependent on the length of the measuring scale used. As the length of the measuring scale goes on reducing, the observed length of the coastline will increase.
Fractals are different from other regular geometric objects because of the way in which they scale. For example, if we double the radius, then the volume of the sphere increases by a factor of eight (23). But if we double the dimensional length of a fractal then the spatial content of the fractal scales by the exponent that is not necessarily an integer. This non-integer exponent is called the fractal dimension of the fractal and is figurative of the huge void spaces which may be present in the fractal objects.
Several works have been carried out to estimate the fractal dimensions of things found in nature. Now a question may arise, why should we study the details of fractal dimension of natural things?. To answer this question, let us discuss the work of Ma et al. 2011 [1]. In their study, Graphene Oxide (GO) in aqueous solution was aerosolized and rapidly dried to produce crumpled nano paper like sheet. These crumpled Graphene balls increase the specific capacitance of the material compared to the flat or wrinkled sheets, and hence it is considered to be a promising ultra-capacitor material [2]. The fractal dimension of the dried and crumpled GO sheet is characterized by using a combined mass-mobility diameter measurement. The results show that the fractal dimension of crumpled Graphene Oxide (GO) nano sheet is 2.54±0.02, which is identical to macroscopic crumpled ball of paper or foil indicating self-similarity at both the nano and macro scale.
Impact of Road-Space-Rationing Method on Regional Air Quality
Source attributed premature mortality from ambient PM2.5 exposure
Aerosol acidity remains high despite declining sulfate concentration
Aerosol burden expected to increase in a warmer world
Challenges in quantifying aerosol-induced changes in cloud properties
Recent Indo-Pacific SST trends suppress rainfall in mid-latitude East Asia
Forthcoming Events
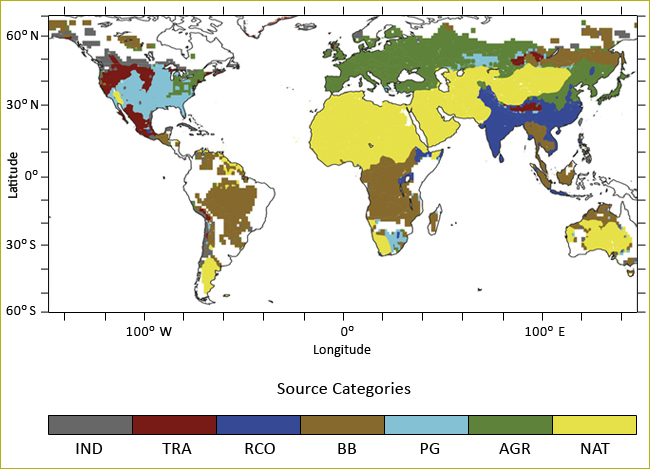
Cover Image: Source categories (IND: industry, TRA: traffic, RCO: residential and commercial energy use, BB: biomass burning, PG: power generation, AGR: agriculture, NAT: natural) responsible for the largest contribution to premature mortality attributed to ambient air pollution exposure (Courtesy: Lelieveld et al., Nature, 2015)
